Trig Sub Chart
Trig Sub Chart - Since − π 2 < θ < π 2 and secθ > 0 over this interval, |. Explore different trigonometric functions that may help you calculate the area. H x = 1 16 + 49x2. See the trig substitution list, the process, and examples with solutions. We can see that the area is. If we change the variable from x to θ by the substitution x = a sin θ,. Web this calculus video tutorial provides a basic introduction into trigonometric substitution. Web learn how to use trig substitution to solve integrals involving square roots, such as a2 x2, x2 + a2, or x2 a2. In general, when other methods fail, use the table. Web the technique of trigonometric substitution comes in very handy when evaluating these integrals. In general, when other methods fail, use the table. In this section, we explore integrals containing expressions of the form √a2 −x2 a 2 − x 2, √a2 +x2 a 2 + x 2, and √x2 −a2 x 2. Calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. G x = 1 36x2 −. It also explains how to. A student uses the following right triangle to determine a trigonometric substitution for an integral. Web this substitution yields √a2 + x2 = √a2 + (atanθ)2 = √a2(1 + tan2θ) = √a2sec2θ = | asecθ | = asecθ. In general, when other methods fail, use the table. See the trig substitution list, the process, and. Identities proving identities trig equations trig inequalities evaluate functions simplify. Web the technique of trigonometric substitution comes in very handy when evaluating these integrals. Web the first thing we’ll need to do here is complete the square on the polynomial to get this into a form we can use a trig substitution on. In this section, we explore integrals containing. Or, \[{\mbox{if }}\theta = {\sec ^{. Identities proving identities trig equations trig inequalities evaluate functions simplify. Explore different trigonometric functions that may help you calculate the area. Web sometimes with inverse substitutions involving trig functions we use \(\theta\) instead of \(u\text{.}\) thus, we would take \(x=\sin\theta\) instead of \(x=\sin u\text{.}\) we would. It also explains how to. Web when using a secant trig substitution and converting the limits we always assume that \(\theta \) is in the range of inverse secant. Explore different trigonometric functions that may help you calculate the area. Mean geometric mean quadratic mean average median. It explains when to substitute x with sin, cos, or sec. A student uses the following right triangle. It also explains how to. We start by completing the square, then make the substitution , followed by the trigonometric substitution of : If we change the variable from x to θ by the substitution x = a sin θ,. Web the first thing we’ll need to do here is complete the square on the polynomial to get this into. Web sometimes with inverse substitutions involving trig functions we use \(\theta\) instead of \(u\text{.}\) thus, we would take \(x=\sin\theta\) instead of \(x=\sin u\text{.}\) we would. Web this substitution yields √a2 + x2 = √a2 + (atanθ)2 = √a2(1 + tan2θ) = √a2sec2θ = | asecθ | = asecθ. This technique uses substitution to rewrite these integrals as. Web introduction to. Web when using a secant trig substitution and converting the limits we always assume that \(\theta \) is in the range of inverse secant. Web the technique of trigonometric substitution comes in very handy when evaluating these integrals. This technique uses substitution to rewrite these integrals as. It explains when to substitute x with sin, cos, or sec. Web learn. In this section, we explore integrals containing expressions of the form √a2 −x2 a 2 − x 2, √a2 +x2 a 2 + x 2, and √x2 −a2 x 2. Explore different trigonometric functions that may help you calculate the area. Mean geometric mean quadratic mean average median. Web sometimes with inverse substitutions involving trig functions we use \(\theta\) instead. We start by completing the square, then make the substitution , followed by the trigonometric substitution of : F x = 1 9 − 16x2. It also explains how to. Which one of the following. Identities proving identities trig equations trig inequalities evaluate functions simplify. Web learn how to use trig substitution to solve integrals involving square roots, such as a2 x2, x2 + a2, or x2 a2. F x = 1 9 − 16x2. H x = 1 16 + 49x2. Which one of the following. Since − π 2 < θ < π 2 and secθ > 0 over this interval, |. A student uses the following right triangle to determine a trigonometric substitution for an integral. A = √ x 2 − 9 d x. Or, \[{\mbox{if }}\theta = {\sec ^{. Identities proving identities trig equations trig inequalities evaluate functions simplify. In general, when other methods fail, use the table. We can see that the area is. If we change the variable from x to θ by the substitution x = a sin θ,. Web this calculus video tutorial provides a basic introduction into trigonometric substitution. Explore different trigonometric functions that may help you calculate the area. It explains when to substitute x with sin, cos, or sec. Web trig substitution investigation | desmos.
Trig Substitution Knowing All the (Tri)Angles Indefinite Integrals

Trig Table
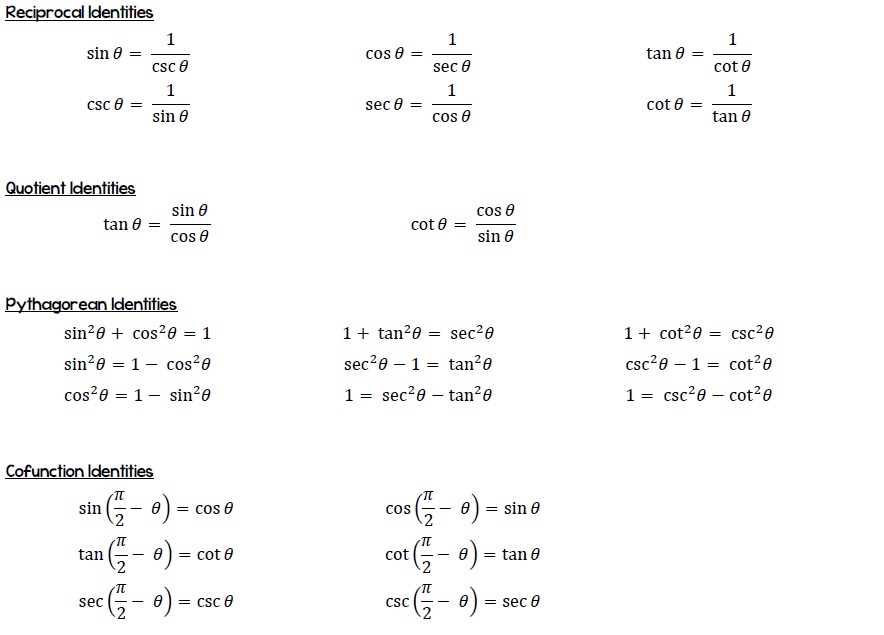
Trig Identities Table of Trigonometric Identities
Trig substitution How to solve? — Krista King Math Online math help

Trigonometry Formula Chart

Integration by Trigonometric Substitution Math Original
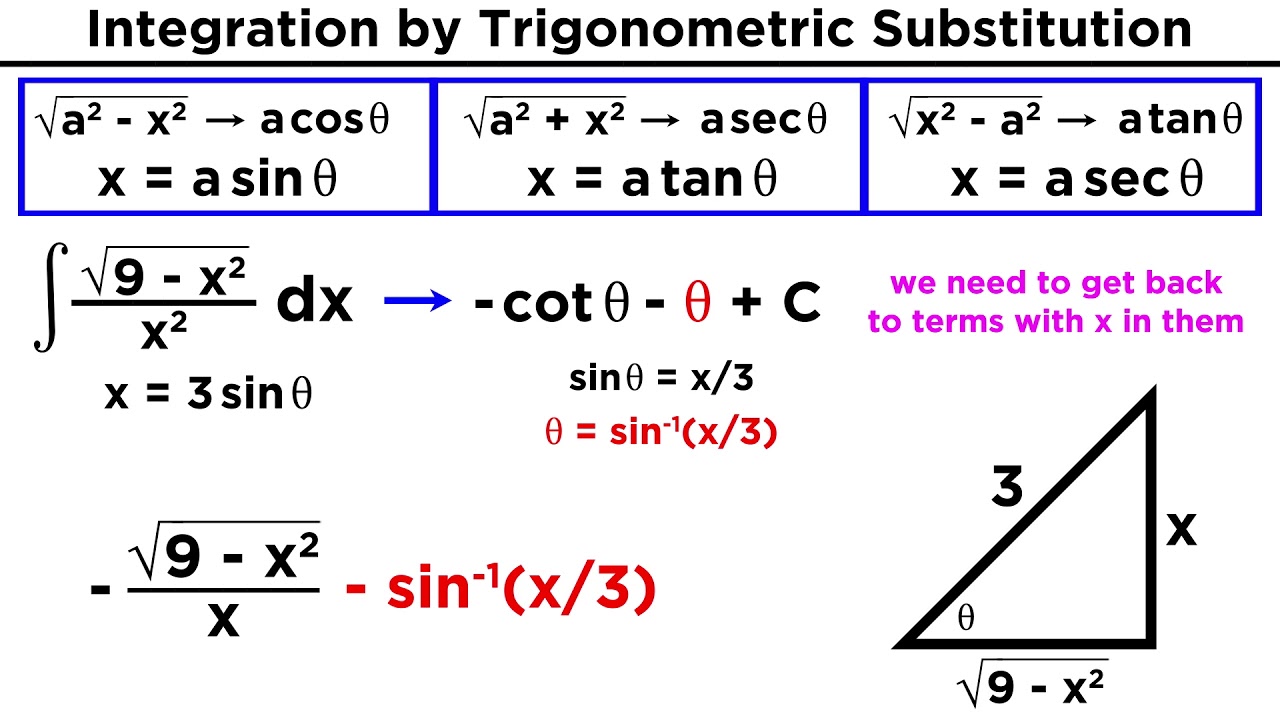
Integration By Trigonometric Substitution YouTube

The Concept of Trig. Substitution YouTube

PPT 7.2 Trig Integrals PowerPoint Presentation, free download ID

Trigonometric Values Chart Pdf
Calculating The Area Of The Shaded Region Requires Evaluating An Integral With A Trigonometric Substitution.
Web The Technique Of Trigonometric Substitution Comes In Very Handy When Evaluating These Integrals.
Web This Substitution Yields √A2 + X2 = √A2 + (Atanθ)2 = √A2(1 + Tan2Θ) = √A2Sec2Θ = | Asecθ | = Asecθ.
Mean Geometric Mean Quadratic Mean Average Median.
Related Post:
