Sign Chart Derivative
Sign Chart Derivative - Zero or undefined (called the critical points ). Web finnifty future derivatives: Another common interpretation is that the derivative gives us the slope of. Web sign chart of the derivative is very useful for findig the maxima, minima, and saddle points of a function. The top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). Web a derivative is positive when the original function is increasing, and negative when the original function is decreasing. It explains how to graph. The derivative of a function f(x) is the function whose value at x is f ′ (x). Type in any function derivative to get the solution, steps and graph. Learn how to draw a sign chart here. Graph of derivative to original function. 4.5.3 use concavity and inflection. Web 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph. The stationary points are written on the sign diagram. Web explore math with our beautiful, free online graphing calculator. Web the derivative of a function describes the function's instantaneous rate of change at a certain point. 4.5.3 use concavity and inflection. Learn how to draw a sign chart here. Web 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph. Graph of derivative to original function. Web sign chart of the derivative is very useful for findig the maxima, minima, and saddle points of a function. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. The derivative of a function f(x) is the function whose value at x is f ′ (x). Web sign diagram for the first derivative. Get a grid. Web use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Explain how the sign of the first derivative affects the shape of a function’s graph. Web to construct a sign chart for a function, first find where the first and second derivatives are. We see that the derivative. The top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). 4.5.2 state the first derivative test for critical points. A sign diagram of the first derivative, f'(𝑥) can be made. We see that the derivative will go from increasing to decreasing or vice versa when f' (x) = 0, or when x=. 4.5.3 use concavity and inflection. Web 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph. Web a derivative is positive when the original function is increasing, and negative when the original function is decreasing. Web this can be done in many ways, but we like using a sign chart. Now determine a sign. Web finnifty future derivatives: 4.5.2 state the first derivative test for critical points. So you look at where the original. Web to construct a sign chart for a function, first find where the first and second derivatives are. Explain how the sign of the first derivative affects the shape of a function’s graph. Now determine a sign chart for the first derivative, f ' : Then determine the sign of the derivative. Web to establish a sign chart (number lines) for f ' , first set f ' equal to zero and then solve for x. Web finnifty future derivatives: 4.5.3 use concavity and inflection. Zero or undefined (called the critical points ). Another common interpretation is that the derivative gives us the slope of. Get the latest updates on finnifty derivatives, future quotes options, f&o analysis, strategy, charts, historical reports. The derivative of a function f(x) is the function whose value at x is f ′ (x). Graph functions, plot points, visualize algebraic equations,. Type in any function derivative to get the solution, steps and graph. A sign diagram of the first derivative, f'(𝑥) can be made. Web sign diagram for the first derivative. 4.5.3 use concavity and inflection. Learn how to draw a sign chart here. This calculus video tutorial provides a basic introduction into curve sketching. A sign diagram of the first derivative, f'(𝑥) can be made. The top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). State the first derivative test for critical points. We see that the derivative will go from increasing to decreasing or vice versa when f' (x) = 0, or when x= 0. Then determine the sign of the derivative. Web use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Explain the concavity test for a function over an open. Explain how the sign of the first derivative affects the shape of a function’s graph. For x =0 and x =2. The stationary points are written on the sign diagram. Get the latest updates on finnifty derivatives, future quotes options, f&o analysis, strategy, charts, historical reports. Get a grid of sign charts for a function and its first and. Web this can be done in many ways, but we like using a sign chart. 4.5.3 use concavity and inflection. Web sign chart of the derivative is very useful for findig the maxima, minima, and saddle points of a function.
Making and Interpreting Sign Charts (First and Second Derivatives

Chart Of Derivatives

Finding Derivatives using Charts and Tables YouTube

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog

How to Understand Sign Diagrams
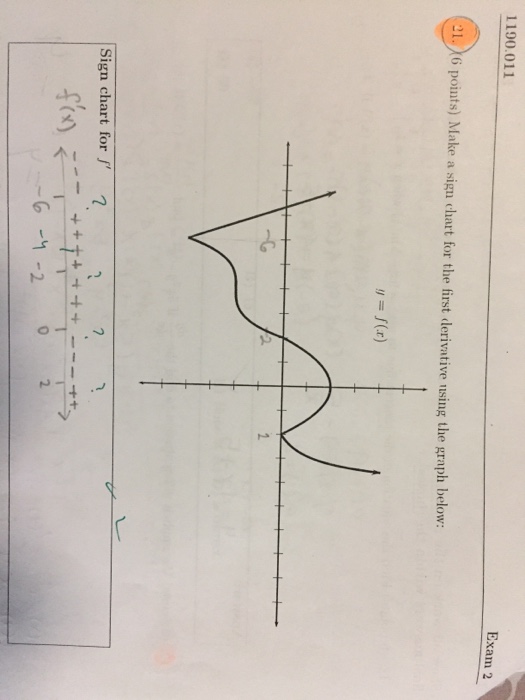
Solved Make a sign chart for the first derivative using the

I made a derivative chart! calculus

Basic derivatives

Free Printable Derivatives Formula Chart (PDF) Math = Love
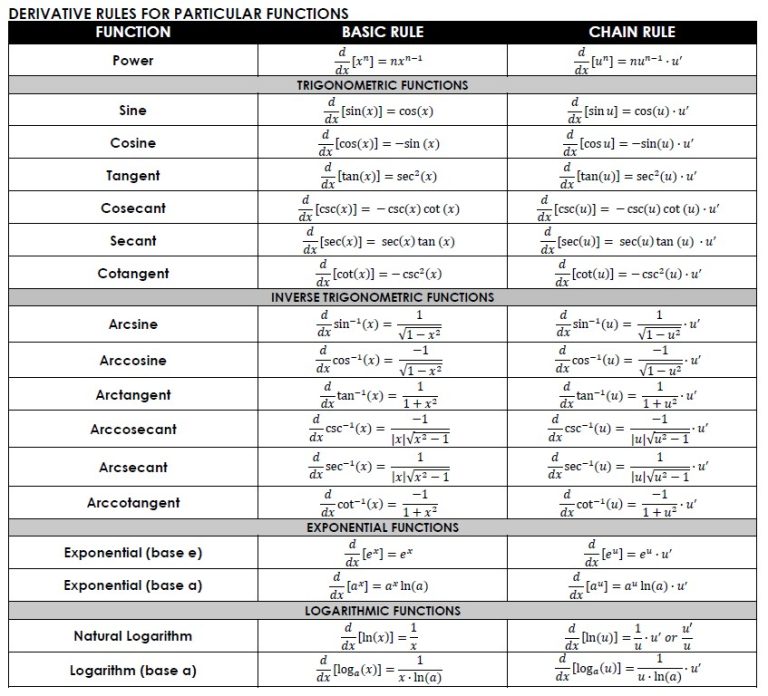
Free Printable Derivatives Formula Chart (PDF) Math = Love
Web To Construct A Sign Chart For A Function, First Find Where The First And Second Derivatives Are.
Type In Any Function Derivative To Get The Solution, Steps And Graph.
Web We Create A First Derivative Sign Chart To Summarize The Sign Of \(F'\) On The Relevant Intervals, Along With The Corresponding Behavior Of \(F\Text{.}\) Figure \(\Pageindex{4}\).
Web The Derivative Of A Function Describes The Function's Instantaneous Rate Of Change At A Certain Point.
Related Post: